量子グラフ理論序説：量子特異点の物理（2-2）

グラフの量子論の設定２

特異点があっても健全な量子力学を行うためには、波動関数と演算子が確率解釈を保証するような一群の基本的性質を満たす必要がある。その一つに観測量は自己共役なヒルベルト空間演算子でなければならないというものがある［1］。ラプラシアンに他ならない自由ハミルトニアン（2.1）についてこれを適用すると、特異点のまわりで確率密度流速が連続でなければならないという結果が得られる。通常の問題では、解が属すべきある種の「物理的に良い性質」の波動関数の集合（例えば二乗可積分でなめらかといったもの）を暗黙のうちに仮定する。そうすると観測量演算子の自己共役性は通常のエルミート性の要求に帰着する。ところが今の文脈でラプラシアンが自己共役であるとの要求は、むしろ「エルミート型の関係」の成立を許す波動関数の集合自体を定める、という事なのである。その意味で「確率密度流速が連続」であるべきとの条件は波動関数の満たすべき量子論のもっとも基本的な要求だと考えて良い。それは

(2.3)

と表せる。いま i 番目の半直線の節点直近の点を 0i であらわし、N次元ヴェクトル Φ、Φ' を

、

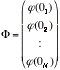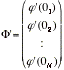(2.4)

で定義すると、確率密度流速保存の条件 (2.3) は

(2.5)

という簡明な表現を得るが、この式はさらに と書き換えられる。ここでL₀ は任意の長さの次元の定数で、式の次元をそろえるために導入された。これは両辺の絶対値の中のヴェクトルがユニタリ行列で変換されることを意味するから、そのN次元ユニタリ行列をU として少し書き換えると

(2.6)

の関係が得られる。ここで次元を理由に「どこからとも無く」定数 L₀ が発生したが、この定数の意味については後節で詳しい議論をおこなう。結局シュレディンガー方程式（2.2）は節点での「多線接合」の性質を規定する式（2.6）に伴われて初めて波動関数を与えることになる。この性質を規定するユニタリ行列U はN² 個のパラメタをもつ。このように測度ゼロの節点での振る舞いを規定するものを「点状相互作用」と呼ぶ事にすると、量子的な点状相互作用としてはN² 個のパラメタ分だけ異なったものが無数に作れるのである。